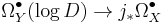Hyperhomology

In homological algebra, the hyperhomology or hypercohomology of a complex of objects of an abelian category is an extension of the usual homology of an object to complexes. It is a sort of cross between the derived functor cohomology of an object and the homology of a chain complex.

Hyperhomology is no longer used much: since about 1970 it has been largely replaced by the roughly equivalent concept of a derived functor between derived categories.

1 Definition
2 The hypercohomology spectral sequences
3 Examples
4 See also
5 References

Definition

We give the definition for hypercohomology as this is more common. As usual, hypercohomology and hyperhomology are essentially the same: one converts from one to the other by changing the direction of all arrows, replacing injective objects with projective ones, and so on.

Suppose that A is an abelian category with enough injectives and F a left exact functor to another abelian category B. If C is a complex of objects of A bounded on the left, the hypercohomology

Hⁱ(C)

of C (for an integer i) is calculated as follows:

Take a quasi-isomorphism Φ : C → I, here I is a complex of injective elements of A.
The hypercohomology Hⁱ(C) of C is then the cohomology Hⁱ(F(I)) of the complex F(I).

The hypercohomology of C is independent of the choice of the quasi-isomorphism, up to unique isomorphisms.

The hypercohomology can also be defined using derived categories: the hypercohomology of C is just the cohomology of F(C) considered as an element of the derived category of B.

The hypercohomology spectral sequences

There are two hypercohomology spectral sequences; one with E₂ term

Hⁱ(R^jF(C))

and the other with E₁ term

R^jF(Cⁱ)

and E₂ term

R^jF(Hⁱ(C))

both converging to the hypercohomology

H^i+j(C),

where R^jF is a right derived functor of F.

Examples

For a variety X over a field k, the second spectral sequence from above gives the Hodge to de Rham spectral sequence for algebraic de Rham cohomology:

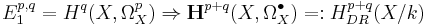
$E_1^{p,q}=H^q(X,\Omega_X^p)\Rightarrow \mathbf{H}^{p%2Bq}(X,\Omega_X^{\bullet})=:H_{DR}^{p%2Bq}(X/k)$

Another example comes from the holomorphic log complex on a complex manifold. Let X be a complex algebraic manifold and 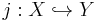$j: X\hookrightarrow Y$ a good compactification. This means that Y is a compact algebraic manifold and 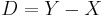$D = Y-X$ is a divisor on $Y$ with simple normal crossings. The natural inclusion of complexes of sheaves

$\Omega^{\bullet}_Y(\log D)\rightarrow j_*\Omega_{X}^{\bullet}$

turns out to be a quasi-isomorphism and induces an isomorphism

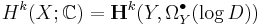$H^k(X;\mathbb{C}) = \mathbf{H}^k(Y, \Omega^{\bullet}_Y(\log D))$ .

References

H. Cartan, S. Eilenberg, Homological algebra ISBN 0691049912
V.I. Danilov (2001), "Hyperhomology functor", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=H/h048480
A. Grothendieck, Sur quelques points d'algèbre homologique Tohoku Math. J. 9 (1957) pp. 119-221

Hyperhomology

Contents

Definition

The hypercohomology spectral sequences

Examples

See also

References